Timing Wheels: An In-depth Exploration

Introduction

The essence of many software systems lies in the precision of their timing. Whether it’s a database handling cache eviction, a networking protocol managing packet retransmissions, or a real-time system coordinating task executions, the capability to manage and execute operations based on time is essential.

Among the myriad of mechanisms devised to address this critical need, timing wheels have emerged as a particularly efficient solution.

This article delves into the heart of timing mechanisms, from basic timer lists to the sophisticated hierarchical timing wheels - we’ll explore their origins, benefits, and practical applications.

History and Origins

Our story begins with the quest for efficient timer management. Traditional mechanisms, while effective for smaller scales, encountered scalability issues as the number of timers grew.

This challenge gave birth to timing wheels - a concept initially introduced in pioneering research papers from institutions like MIT.

As the complexity and scale of our systems advanced, the need for robust timer management solutions grew, leading to the evolution and refinement of timing wheels which have become a cornerstone in high-performance systems design.

A Journey Through Timing Mechanisms

Let’s explore this evolution.

1. Unordered Timer List

• Description: A simplistic approach where timers are stored in an unordered list. To handle expirations, the entire list is scanned.
• Mathematical Complexity: Searching has a time complexity of O(n).
• Practical Usage: Suitable for systems with a minimal number of timers.
• Diagram:

2. Ordered Timer List

• Description: An improvement over the unordered list, timers are stored in an ordered fashion based on expiration times.
• Mathematical Complexity: Insertion is O(n), but accessing the nearest timer is O(1).
• Practical Usage: Efficient for scenarios with frequent timer expirations but infrequent insertions.
• Diagram:

3. Timer Trees

• Description: Timers are organised in a balanced tree structure, offering better overall performance than simple lists.
• Mathematical Complexity: Operations like insertion and extraction are O(logn).
• Practical Usage: Suitable for systems that need faster insertion and deletion operations than ordered lists can provide.
• Diagram:

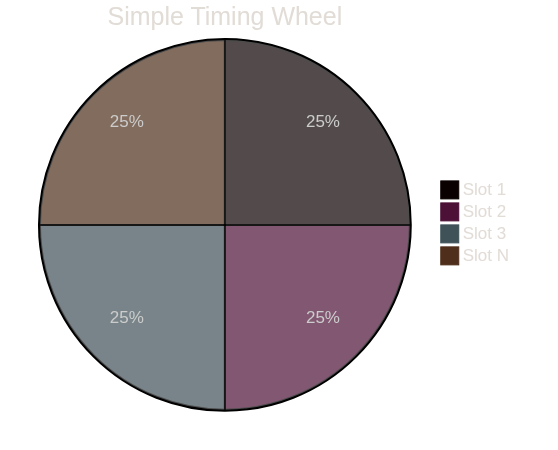
4. Simple Timing Wheels

• Description: A circular buffer structure that enhances timer management by offering constant-time operations.
• Mathematical Complexity: Both insertion and expiration handling are O(1).
• Practical Usage: Ideal for high-performance systems where efficiency is paramount.
• Diagram:

5. Hashing Wheel with Ordered Timer Lists

• Description: A hybrid approach that hashes timers into slots, with each slot maintaining an ordered list of timers.
• Mathematical Complexity: Combines the complexities of hashing and ordered lists.
• Practical Usage: Efficient in scenarios where timers are dispersed over a wide range of expiration times.
• Diagram:

6. Hashing Wheel with Unordered Timer Lists

• Description: Similar to its ordered counterpart but with unordered lists in each slot.
• Mathematical Complexity: Faster insertion but slower expiration handling than its ordered counterpart.
• Practical Usage: Suitable for systems where insertion frequency is higher than expiration handling.
• Diagram:

7. Hierarchical Timing Wheels

• Description: An extension of simple timing wheels to handle a wider range of expiration times without increasing granularity.
• Mathematical Complexity: While insertion remains O(1), handling timers that get promoted to higher-level wheels might add overhead. However, it remains efficient for a broad range of timer expirations.
• Practical Usage: Systems requiring efficient timer management over both short and long durations benefit immensely from hierarchical wheels.
• Diagram:

What is a Timing Wheel?

Stepping away from the theoretical and diving into the practical, let’s demonstrate the concept of a timing wheel.

Definition and Concept

Imagine a circular buffer, akin to the face of a clock. Each slot on this “clock” represents a time interval, and tasks or events are placed into these slots based on when they need to be executed.

As time progresses, a pointer (or “hand”) rotates around this clock, and when it points to a slot, any tasks within that slot are executed.

Code Example in Go

This Golang snippet provides a rudimentary representation of a timing wheel. It demonstrates how tasks can be inserted and how they are executed when the “tick” function is called.

1
type TimerTask struct {
2
    Execute func()
3
}
4

5
type TimingWheel struct {
6
    slots []TimerTask
7
    currentPosition int
8
}
9

10
func NewTimingWheel(numSlots int) *TimingWheel {
11
    return &TimingWheel{
12
        slots: make([]TimerTask, numSlots),
13
        currentPosition: 0,
14
    }
15
}
16

17
func (tw *TimingWheel) Insert(task TimerTask, position int) {
18
    tw.slots[position] = task
19
}
20

21
func (tw *TimingWheel) Tick() {
22
    task := tw.slots[tw.currentPosition]
23
    task.Execute()
24
    tw.currentPosition = (tw.currentPosition + 1) % len(tw.slots)
25
}

Advantages of Timing Wheels

Peeling back the layers, let’s delve into what makes timing wheels an effective solution in system design.

Scalability

Timing wheels excel in scenarios where there are a large number of timers to be managed. Traditional timer data structures, like heaps, may suffer from performance degradation as the number of timers increases. Timing wheels offer a more scalable alternative.

Constant Time Complexity

The insertion and deletion of timers in a timing wheel are typically constant-time operations, which is a significant advantage over other data structures that may require logarithmic or linear time.

Memory Efficiency

Given the fixed size of the timing wheel, memory allocations are predictable and minimal, leading to reduced overhead and better performance.

Applications in System Design and Software Engineering

Diving into real-world applications, let’s explore where timing wheels prove their usefulness.

Networking

In the transmission of data packets on a network, timing wheels choreograph events like packet retransmissions in protocols such as TCP. Their efficient timer management ensures seamless communication.

Distributed Systems

In complex domain of distributed systems, where numerous nodes collaborate, timing wheels handle tasks like heartbeat checks, lease renewals, and more. Their precision ensures system consistency and resilience.

Real-time Systems

Precision is the soul of real-time systems. From robotics to media playback, tasks need execution at exact intervals. Timing wheels prove highly effective at this.

Databases

Databases, the backbone of many modern applications, rely on timing wheels for functions like cache eviction and garbage collection. This ensures data retrieval remains swift and system health optimal.

Real-World Scenario: Web Server Request Timeouts

Imagine you’re building a web server in Golang. This server interacts with several services, databases, and even external APIs.

To ensure that a slow or unresponsive service doesn’t cause the entire server to hang, you implement request timeouts.

The Problem

You receive thousands of requests per second, each with its own timeout. Managing these timeouts efficiently is crucial to ensure smooth server operations.

The Solution

Implementing a timing wheel to handle these timeouts.

1. Every incoming request gets a timer set for its timeout duration.
2. If a request is completed before its timeout, its timer is cancelled.
3. If the timer expires, the request is terminated, and an appropriate timeout response is sent back.

Implementation in Golang

Let’s draft a basic implementation using a simplified timing wheel:

1
package main
2

3
import (
4
 "fmt"
5
 "time"
6
)
7

8
type Request struct {
9
 ID      int
10
 Timeout time.Duration
11
 Cancel  chan bool
12
}
13

14
type TimingWheel struct {
15
 slots          []chan Request
16
 currentPosition int
17
 tickDuration   time.Duration
18
}
19

20
func NewTimingWheel(numSlots int, tickDuration time.Duration) *TimingWheel {
21
 tw := &TimingWheel{
22
  slots:          make([]chan Request, numSlots),
23
  tickDuration:   tickDuration,
24
  currentPosition: 0,
25
 }
26
 for i := range tw.slots {
27
  tw.slots[i] = make(chan Request, 10) // assuming a buffer size of 10 for each slot
28
 }
29
 return tw
30
}
31

32
func (tw *TimingWheel) Insert(req Request) {
33
 position := (tw.currentPosition + int(req.Timeout/tw.tickDuration)) % len(tw.slots)
34
 tw.slots[position] <- req
35
}
36

37
func (tw *TimingWheel) Start() {
38
 ticker := time.NewTicker(tw.tickDuration)
39
 defer ticker.Stop()
40

41
 for range ticker.C {
42
  slot := tw.slots[tw.currentPosition]
43
  close(slot)
44
  tw.slots[tw.currentPosition] = make(chan Request, 10)
45

46
  // Handle expired requests
47
  for req := range slot {
48
   select {
49
   case <-req.Cancel:
50
    // Request was completed in time
51
   default:
52
    fmt.Printf("Request %d timed out!\n", req.ID)
53
   }
54
  }
55

56
  tw.currentPosition = (tw.currentPosition + 1) % len(tw.slots)
57
 }
58
}
59

60
func main() {
61
 tw := NewTimingWheel(60, time.Second) // 60 slots, 1 second per tick
62

63
 go tw.Start()
64

65
 // Simulating incoming requests
66
 for i := 0; i < 100; i++ {
67
  req := Request{
68
   ID:      i,
69
   Timeout: time.Duration(5+i%10) * time.Second, // random timeouts between 5 to 15 seconds
70
   Cancel:  make(chan bool),
71
  }
72
  tw.Insert(req)
73
 }
74

75
 // Simulating some requests completing before timeout
76
 time.Sleep(8 * time.Second)
77
 for i := 0; i < 50; i++ {
78
  close(tw.slots[i%60][i].Cancel)
79
 }
80

81
 // Let the program run for a while
82
 time.Sleep(2 * time.Minute)
83
}

This is a rudimentary implementation to demonstrate the concept. In a real-world scenario, you’d integrate this with your web server’s request handling, ensuring that each request has a timer associated with it in the timing wheel.

The advantage here is the efficiency in handling a large number of timeouts without significant overhead.

Conclusion

As our digital landscapes evolve, transitioning towards real-time and data-intensive ecosystems, the significance of efficient timer management mechanisms cannot be understated. Timing wheels offer a robust solution to this problem, and their applications are widespread.

They are yet another useful tool in the software engineers arsenal, and I hope this article gave you a good introduction to timing wheels and their applications. If you have any questions or feedback, feel free to reach out to me!

References

1. ACM: Efficient Timer Management
2. Confluent: Apache Kafka and Hierarchical Timing Wheels
3. GitHub: Golang Implementation of Timing Wheel
4. The Morning Paper: Hashed and Hierarchical Timing Wheels
5. Image by Steffen L. from Pixabay